Tag: netvizz

Visto l’interesse destato dall’analisi del gruppo Facebook dell’Università di Urbino ho deciso di estendere questa visualizzazione per includere più gruppi. L’idea è quella di rappresentare le relazioni di amicizia dei più rappresentativi gruppi Facebook di Urbino.
In una prima fase ho dunque dovuto cercare e selezionare i gruppi da prendere in considerazione.
Sono dunque partito da una semplice ricerca con la chiave urbino nel motore interno di Facebook limitando i risultati ai soli gruppi. Degli oltre 364 gruppi restituiti, ho deciso di escludere tutti quelli che, dal titolo, sembravano chiaramente riferirsi a realtà più grandi (ad esempio tutti quelli Pesaro e Urbino). Ho inoltre deciso di prendere in considerazione solo i gruppi con oltre 50 membri. Di questi alcuni erano aperti ed altri chiusi. Per quelli aperti mi sono semplicemente unito al gruppo, per quelli chiusi ho richiesto l’autorizzazione a diventare membro (solo in un caso mi è stato chiesto il perché ed ho spiegato che stavo conducendo una ricerca). Ho avuto così accesso ai dati di 72 gruppi. Per ciascuno di essi ho scaricato il grafo delle relazioni intergruppo (usando netvizz) e aggregato i risultati in un unico file .gdf copiando in questo file la lista dei membri del gruppo e quella delle loro relazioni. Questa procedura ha causato ovviamente la duplicazione di molti nodi con il rispettivo numero identificativo. Questa duplicazione non ha tuttavia causato problemi all’atto dell’importazione in Gephi durante la quale i nodi duplicati sono stati automaticamente eliminati.
Il grafo risultato dall’aggregazione di tutte le relazioni fra i membri dei gruppi presi in considerazione consiste alla fine di 14014 nodi e 175188 archi.
Su questo grafo ho calcolato i soliti indici di centralità (eigenvector, betweenness, closeness ed eccentricity) e la modularity per individuare le comunità.
Ho inoltre posizionato i nodi utilizzando l’algortimo ForceAtlas 2 (con il paramento Gravity a 100 per evitare una eccessiva disgregazione).
L’analisi della modularità, definita come una misura di quanto bene una rete possa essere scomposta in comunità modulari, si attesta intorno allo 0,6 ed il numero di comunità identificato oscilla (si tratta di algoritmo randomizzato che genera risultati diversi ogni volta che viene eseguito) intorno alle 1000.

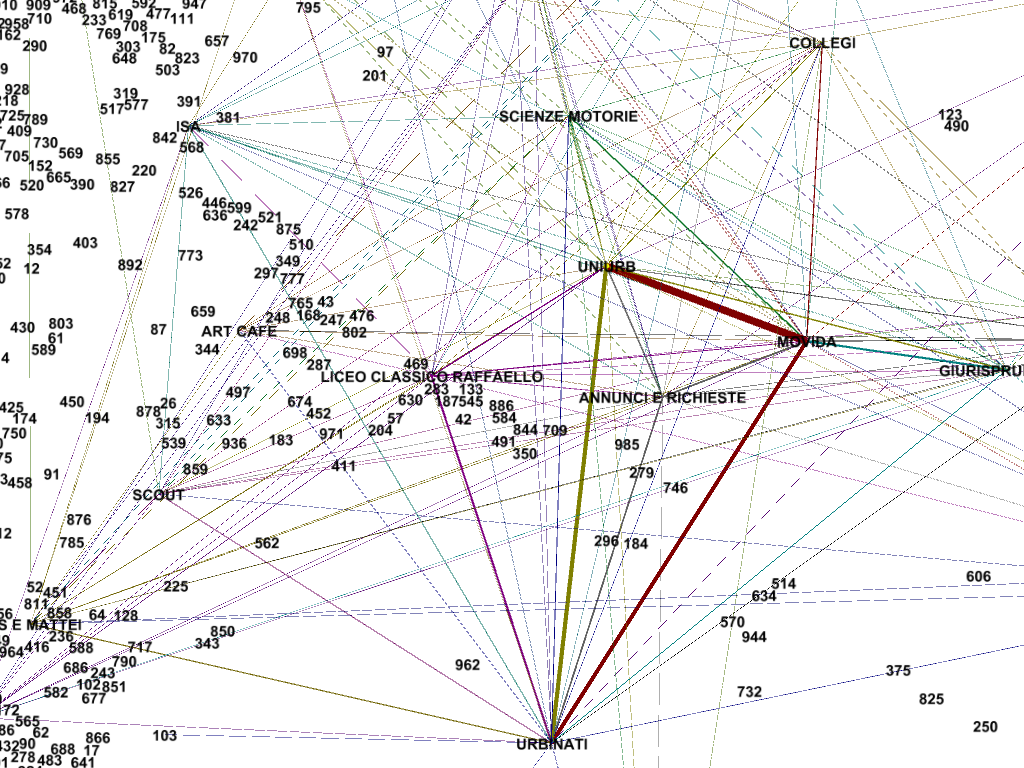
Da questo migliaio di comunità ne emergono tre che da sole raccolgono quasi il 50% dei nodi.
Si tratta di quelle che ho identificato come UNIURB (15,5% e colore Verde), URBINATI (15,02% Blu) e MOVIDA (13,15% Rosso). Significativa inoltre la dimensione del gruppo del COLLEGI (7,34% Giallo), GIURISPRUDENZA (5,41% Azzurro), ANNUNCI E RICHIESTE (5,35% Grigio), LICEO CLASSICO RAFFAELLO (5,26% Fucsia). Fra le altre comunità che ho identificato figurano inoltre quella dell’ISIA, dell’Istituto d’Arte, dell’Istituto per la Formazione al Giornalismo e quella degli studenti Greci.

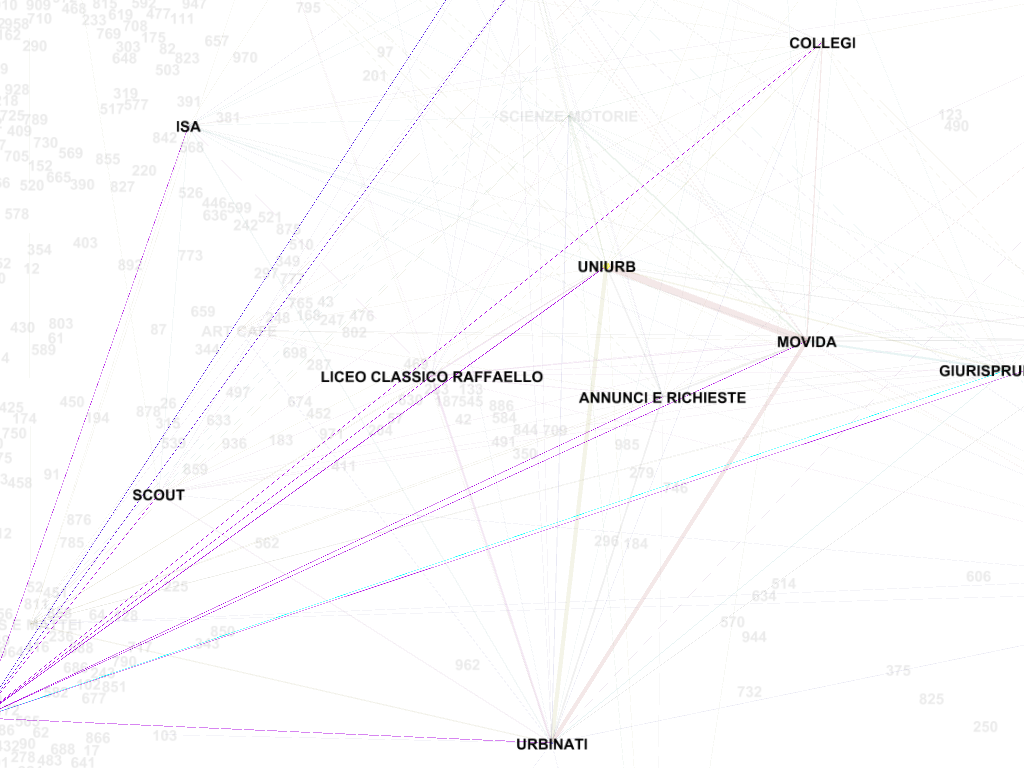
Nelle immagini che seguono due visualizzazioni dei 250 utenti meglio connessi secondo, rispettivamente, la metrica della betweenness centrality e dell’eigenvector centrality.


Infine, visto che zoom.it si rifiuta di creare l’immagine zoommabile, potete scaricare le visualizzazioni totali in formto pdf con la dimensione dei nodi legate alla betweenness e all’eigenvector centrality (i nomi, in queste visualizzazioni complessive, sono stati volutamente rimossi per questioni di privacy).Visto l’interesse destato dall’analisi del gruppo Facebook dell’Università di Urbino ho deciso di estendere questa visualizzazione per includere più gruppi. L’idea è quella di rappresentare le relazioni di amicizia dei più rappresentativi gruppi Facebook di Urbino.
In una prima fase ho dunque dovuto cercare e selezionare i gruppi da prendere in considerazione.
Sono dunque partito da una semplice ricerca con la chiave urbino nel motore interno di Facebook limitando i risultati ai soli gruppi. Degli oltre 364 gruppi restituiti, ho deciso di escludere tutti quelli che, dal titolo, sembravano chiaramente riferirsi a realtà più grandi (ad esempio tutti quelli Pesaro e Urbino). Ho inoltre deciso di prendere in considerazione solo i gruppi con oltre 50 membri. Di questi alcuni erano aperti ed altri chiusi. Per quelli aperti mi sono semplicemente unito al gruppo, per quelli chiusi ho richiesto l’autorizzazione a diventare membro (solo in un caso mi è stato chiesto il perché ed ho spiegato che stavo conducendo una ricerca). Ho avuto così accesso ai dati di 72 gruppi. Per ciascuno di essi ho scaricato il grafo delle relazioni intergruppo (usando netvizz) e aggregato i risultati in un unico file .gdf copiando in questo file la lista dei membri del gruppo e quella delle loro relazioni. Questa procedura ha causato ovviamente la duplicazione di molti nodi con il rispettivo numero identificativo. Questa duplicazione non ha tuttavia causato problemi all’atto dell’importazione in Gephi durante la quale i nodi duplicati sono stati automaticamente eliminati.
Il grafo risultato dall’aggregazione di tutte le relazioni fra i membri dei gruppi presi in considerazione consiste alla fine di 14014 nodi e 175188 archi.
Su questo grafo ho calcolato i soliti indici di centralità (eigenvector, betweenness, closeness ed eccentricity) e la modularity per individuare le comunità.
Ho inoltre posizionato i nodi utilizzando l’algortimo ForceAtlas 2 (con il paramento Gravity a 100 per evitare una eccessiva disgregazione).
L’analisi della modularità, definita come una misura di quanto bene una rete possa essere scomposta in comunità modulari, si attesta intorno allo 0,6 ed il numero di comunità identificato oscilla (si tratta di algoritmo randomizzato che genera risultati diversi ogni volta che viene eseguito) intorno alle 1000.
Da questo migliaio di comunità ne emergono tre che da sole raccolgono quasi il 50% dei nodi.
Si tratta di quelle che ho identificato come UNIURB (15,5% e colore Verde), URBINATI (15,02% Blu) e MOVIDA (13,15% Rosso). Significativa inoltre la dimensione del gruppo del COLLEGI (7,34% Giallo), GIURISPRUDENZA (5,41% Azzurro), ANNUNCI E RICHIESTE (5,35% Grigio), LICEO CLASSICO RAFFAELLO (5,26% Fucsia). Fra le altre comunità che ho identificato figurano inoltre quella dell’ISIA, dell’Istituto d’Arte, dell’Istituto per la Formazione al Giornalismo e quella degli studenti Greci.
Nelle immagini che seguono due visualizzazioni dei 250 utenti meglio connessi secondo, rispettivamente, la metrica della betweenness centrality e dell’eigenvector centrality.


Infine, visto che zoom.it si rifiuta di creare l’immagine zoommabile, potete scaricare le visualizzazioni total in pdf con la dimensione dei nodi legate alla betweenness e all’eigenvector centrality (i nomi, in queste visualizzazioni complessive, sono stati volutamente rimossi per questioni di privacy).Visto l’interesse destato dall’analisi del gruppo Facebook dell’Università di Urbino ho deciso di estendere questa visualizzazione per includere più gruppi. L’idea è quella di rappresentare le relazioni di amicizia dei più rappresentativi gruppi Facebook di Urbino.
In una prima fase ho dunque dovuto cercare e selezionare i gruppi da prendere in considerazione.
Sono dunque partito da una semplice ricerca con la chiave urbino nel motore interno di Facebook limitando i risultati ai soli gruppi. Degli oltre 364 gruppi restituiti, ho deciso di escludere tutti quelli che, dal titolo, sembravano chiaramente riferirsi a realtà più grandi (ad esempio tutti quelli Pesaro e Urbino). Ho inoltre deciso di prendere in considerazione solo i gruppi con oltre 50 membri. Di questi alcuni erano aperti ed altri chiusi. Per quelli aperti mi sono semplicemente unito al gruppo, per quelli chiusi ho richiesto l’autorizzazione a diventare membro (solo in un caso mi è stato chiesto il perché ed ho spiegato che stavo conducendo una ricerca). Ho avuto così accesso ai dati di 72 gruppi. Per ciascuno di essi ho scaricato il grafo delle relazioni intergruppo (usando netvizz) e aggregato i risultati in un unico file .gdf copiando in questo file la lista dei membri del gruppo e quella delle loro relazioni. Questa procedura ha causato ovviamente la duplicazione di molti nodi con il rispettivo numero identificativo. Questa duplicazione non ha tuttavia causato problemi all’atto dell’importazione in Gephi durante la quale i nodi duplicati sono stati automaticamente eliminati.
Il grafo risultato dall’aggregazione di tutte le relazioni fra i membri dei gruppi presi in considerazione consiste alla fine di 14014 nodi e 175188 archi.
Su questo grafo ho calcolato i soliti indici di centralità (eigenvector, betweenness, closeness ed eccentricity) e la modularity per individuare le comunità.
Ho inoltre posizionato i nodi utilizzando l’algortimo ForceAtlas 2 (con il paramento Gravity a 100 per evitare una eccessiva disgregazione).
L’analisi della modularità, definita come una misura di quanto bene una rete possa essere scomposta in comunità modulari, si attesta intorno allo 0,6 ed il numero di comunità identificato oscilla (si tratta di algoritmo randomizzato che genera risultati diversi ogni volta che viene eseguito) intorno alle 1000.
Da questo migliaio di comunità ne emergono tre che da sole raccolgono quasi il 50% dei nodi.
Si tratta di quelle che ho identificato come UNIURB (15,5% e colore Verde), URBINATI (15,02% Blu) e MOVIDA (13,15% Rosso). Significativa inoltre la dimensione del gruppo del COLLEGI (7,34% Giallo), GIURISPRUDENZA (5,41% Azzurro), ANNUNCI E RICHIESTE (5,35% Grigio), LICEO CLASSICO RAFFAELLO (5,26% Fucsia). Fra le altre comunità che ho identificato figurano inoltre quella dell’ISIA, dell’Istituto d’Arte, dell’Istituto per la Formazione al Giornalismo e quella degli studenti Greci.
Nelle immagini che seguono due visualizzazioni dei 250 utenti meglio connessi secondo, rispettivamente, la metrica della betweenness centrality e dell’eigenvector centrality.


Infine, visto che zoom.it si rifiuta di creare l’immagine zoommabile, potete scaricare le visualizzazioni total in pdf con la dimensione dei nodi legate alla betweenness e all’eigenvector centrality (i nomi, in queste visualizzazioni complessive, sono stati volutamente rimossi per questioni di privacy).